|
|
| Artikler |
|
Robot Netværk Tele Installationer Lys Komponenter Elektronik Cases Håndværk Elektroteknik Historien Af interesse |
| Diverse |
|
Opslag Billedopslag FAQ Video Links Om |
 Tilpasset søgning |
Logaritmisk skala
| Dokument oprettet: | 9 Apr 2006 |
| Senest ændret: | 24 Apr 2021 |
| Forfatter: | Cubus |
 Karakteristikker ses ofte afsat i et logaritmisk koordinatsystem. Den logaritmiske skala udmærker sig ved, at værdier inden for et stort talområde kan aflæses med god præcision inden for alle intervaller. Fx kan man på en Siemens tid-strøm karakteristik (afsat i et dobbeltlogaritmisk koordinatsystem) for en 10 A gL/gG neozed sikring aflæse, at sikringen ved en strømstyrke på 20 A smelter over efter 400 sekunder. I det samme koordinatsystem kan man med lignende præcision fastslå, at en 80 A sikring ved en strømstyrke på 2000 A smelter over på kun 0,005 sekunder. Aflæsninger med så stor spændvidde og præcision ville ikke være mulige i et almindeligt lineært koordinatsystem, hvis graferne skulle holde sig inden for fx et stykke A4-papir.
Karakteristikker ses ofte afsat i et logaritmisk koordinatsystem. Den logaritmiske skala udmærker sig ved, at værdier inden for et stort talområde kan aflæses med god præcision inden for alle intervaller. Fx kan man på en Siemens tid-strøm karakteristik (afsat i et dobbeltlogaritmisk koordinatsystem) for en 10 A gL/gG neozed sikring aflæse, at sikringen ved en strømstyrke på 20 A smelter over efter 400 sekunder. I det samme koordinatsystem kan man med lignende præcision fastslå, at en 80 A sikring ved en strømstyrke på 2000 A smelter over på kun 0,005 sekunder. Aflæsninger med så stor spændvidde og præcision ville ikke være mulige i et almindeligt lineært koordinatsystem, hvis graferne skulle holde sig inden for fx et stykke A4-papir.
Denne artikel handler om, hvordan den logaritmiske skala er opbygget og hvordan den aflæses.
Opbygning af en logaritmisk skala
På nedenstående diagram, udført i et almindeligt koordinatsystem, ses en kurve over funktionen y = log x. Logaritmen til et tal er pr definition det tal, som 10 skal opløftes i for at give tallet. Logaritmen til 1 er fx lig med 0, fordi 100 er 1.Det ses i venstre side af diagrammet, at der kan fremtrylles en ny uensartet skalaopdeling, når de enkelte tal på x-aksen føres ud på y-aksen, hvor kurven y = log x skæres. Den herved dannede skala kaldes for en logaritmisk skala.

| Princippet for opbygning af den logaritmiske skala. Den logaritmiske skala, der ses ude til venstre, har ikke lige stor afstand mellem lige store talintervaller, som det fx tydeligt fremgår ved sammenligning af afstanden mellem 1 og 2, henholdsvis 9 og 10. |
På en lineær skala er afstanden, målt fx i cm, lige stor mellem lige store talintervaller. En målt afstand mellem 10 og 20 vil være den samme som mellem 130 og 140, da begge talpar udgør et talinterval på 10.
På en logaritmisk skala forholder det sig anderledes. På en logaritmisk skala måles en enslydende afstand mellem talintervaller, der udgør lige store forhold. Med et centimetermål vil der kunne måles den samme afstand mellem 2 og 1 og mellem 8 og 4, da forholdene mellem de to talintervaller er ens: 2/1 = 2 og 8/4 = 2. Den samme afstand må følgelig også kunne måles mellem 10.000 og 5.000!
Logaritmiske skalaer udgøres af et antal dekader, dvs intervaller mellem to på hinanden følgende potenser af 10. Skalaen kan fx dække et område fra 10-3 til 104 (0,001 til 10.000).
Aflæsning sådan cirka
Sædvanligvis findes der støttelinjer i det logaritmiske koordinatsystem, der giver en god idé om en korrekt aflæsningsværdi. Men ellers kan man på ovenstående diagram se, at fx tallet 2 på den logaritmiske skala ligger godt 30 % oppe i dekaden fra 1 til 10 (ved 0,3 på den lineære skala fra 0,0 til 1,0). Tallet 20 vil ligeledes ligge godt en tredjedel oppe i dekaden mellem 10 og 100 osv.Tallene 5, 50, 500 osv ligger godt 70 % oppe i deres respektive dekader, altså lidt mere end to tredjedele oppe.
Lidt under midten i en dekade på en logaritmisk skala befinder sig 3, 30, 300 osv.
Aflæsning mere præcist
Placering af given værdi på skalaen
På nedenstående billede ses et udklip fra en tid-strøm kurve over gL/gG diazed sikringer. Enheden på y-aksen er sekunder. På x-aksen, der ikke ses, er enheden ampere. En dekade (her 100 til 101) er med en lineal målt til 25 mm.Det ønskes at aflæse en sikrings smeltestrøm ved tiden 5 sekunder, hvor der imidlertid ikke er en hjælpelinje at gå ud fra. Havde der været tale om en lineær skala ville 5 ligge præcis mellem 4 og 6. På en logaritmisk skala kan den geometriske midte mellem to punkter udregnes som kvadratroden af endepunkternes produkt, altså i dette tilfælde kvrod (4 · 6) = 4,90. Hvor skal 5 placeres på den logaritmiske skala?

| Udsnit af smeltetidskurver i dobbeltlogaritmisk koordinatsystem. Tiden 5 sekunder befinder sig på y-aksen et sted mellem 4 og 6, men hvor mere præcist? |
Logaritmen til 5 er ca 0,70. Ved at gange dekadens målte 25 mm med 0,70 findes, hvor langt oppe fra dekadens start 5 skal afsættes. Regnestykket giver en afstand af ca 17,5 mm.
Logaritmen til 50 er 1,70, til 500 er den 2,70 osv. Hvis en dekadeafstand multipliceres med disse tal, er det 100, der danner udgangspunkt for den eftersøgte afstand. Men som det ses er decimalerne ved både 5, 50, 500... enslydende, og hvis der ses bort fra heltallet, og altså blot ganges med decimalerne, er det den aktuelle dekades start, der skal måles fra.
Logaritmen til 0,5 er -0,30 og logaritmen til 0,05 er -1,30. Igen er det 100, der danner udgangspunkt for udmålingen. Hvis der ses bort fra heltallet tages målet fra øverst i den aktuelle dekade og nedefter. 0,5, 0,05 osv skal altså afsættes 30 % af en dekadeafstand nedefter, hvilket passer som fod i hose med at gå 70 % op fra dekadens start, som nævnt ovenfor.
Aflæsning af given værdi
I nedenstående udsnit af tid-strøm karakteristikken er det en strømstyrke fra et punkt på en kurve, der skal udfindes. En dekade er her målt op til 50 mm (102 til 103). Afstanden fra den aktuelle dekades start til den ukendte strømstyrke er målt til 11,8 mm.
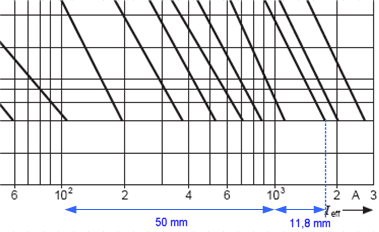
| Strømstyrken i det udvalgte punkt på kurven ligger et sted mellem 1000 og 2000 A, men hvad er strømværdien sådan mere præcist? |
For beregningsmæssigt at finde strømstyrken ved det udvalgte punkt, skal den aktuelle dekades startværdi (her 103) ganges med 10 opløftet i forholdet mellem den målte afstand ud til målepunktet og den målte afstand i en dekade. Resultatet er altså som følger:
1000 · 10(11,8/50) = 1722 A
Interne links til emner i denne artikel: Eksterne links til emner i denne artikel:
- Tiden krymper! [Jørgen Ebert]
- Logaritmisk skala [DMU]
| Home | | | Copyright © 2002-2025 Cubus | cubusadsldk@gmail.com |